
The quadratic formula
What is it?
The quadratic formula can be used to directly find the x-intercepts if we are given the standard form.
It is written as...
Standard form is written as y=ax^2+bx+c, and the "a", "b", and "c" are the values that we plug in the formula.
Let's try an example!
y=6x^2+x-2
-
Set y=0
-
0=6x^2+x-2
-
The "a" value is 6.
-
The "b" value is 1.
-
The "c" value is -2.
-
Substitute these values into the equation.
-
Solve inside the square root sign.
-
Add 1 and 48.
-
Find the square root.
-
x=(-1+7)/-4
-
First do (-1+7)/-4, and then do (-1-7)/-4.
-
x=(-1+7)/-4
-
x=6/-4
-
x=-1.5
-
x=(-1-7)/-4
-
x=-8/-4
-
x=2
We have found the x-intercepts, and using this we can find the axis of symmetry, by adding the
x-intercepts and dividing by 2.
-
(2+(-1.5))/2
-
(2-1.5)/2
-
0.5/2
-
x=0.25
The axis of symmetry is the "x" value of the vertex, so now we need to find the "y" value in order to graph.
We can substitute the "x" value in the original equation, and solve for "y".
y=6x^2+x-2
y=6(0.25)^2+0.25-2
y=6(0.0625)+0.25-2
y=0.375+0.25-2
y=0.625-2
y=(-1.375)
Vertex is (0.25, -1.375).
Video for better understanding!
Try these examples....
1) 0=5x^2-7x+2
2) 2=6x^2+x
3) 0=9x^2-24x+16
Answers are...
1) x=1 and x=2/5
2) x=0.5 and x=-0.66
3) x=1.38 and x=1.3
Video time!
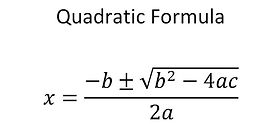
The quadratic
formula
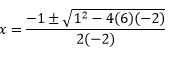
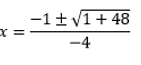
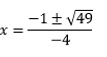
Note: In order to use the quadratic rule, you must always make the "y" equal to 0 if it is not 0.
Word problem
PART A
Word Problem
PART B
Remember the "plus/minus" rule, where we have to add and subtract the same number.
Using the
quadratic formula
 |  |
|---|---|
 |