From graph to the equation

 

What if we are given the graph and we need to find the equation?

• Look for the x-intercepts on the graph, and substitute them for "r" and "s" in the equation, however, make sure you change the signs when you do this.

 

Wait, we are forgetting the "a" value!

How do we find that?

• We substitute the "x" value of the vertex for "x" in the equation, and substitute the "y" value of the vertex for "y" in the equation.

• Then, solve for "a"

 

Let's try an example!

If the vertex of a parabola is (2,3), and two x-intercepts of (8,0) and (4,0).

• Substitute the x-intercepts, so it would be y=a(x-8) (x-4)

• Now substitute the "y" value of the vertex for the "y" value in the equation, making it 3=a(x-8) (x-4)

• Substitute the "x" value of the vertex for the "x" value in the equation, making it 3=a(2-8) (2-4).

• Solve for "a"

• 3=a(-6) (-2)

• 3=a(12)

• 3/12=a(12)/12

• a=3/12

• a=1/4

• a=0.25

 

Then we would be ready with our equation, created by looking at the graph!

 

Now example time!

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

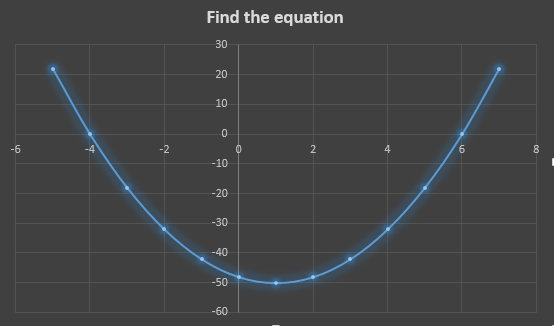
The vertex is shown, and it is (1,-50).

The x-intercepts (points where the graph crosses the x-axis) are also shown.

They are (6,0) and (-4,0).

• Now substitute the x-intercepts, and switch the signs when you do so.

• That will make it y=a(x-6) (x+4).

• Find the "a" value by substituting the "x" value of the vertex for the "x" value in the equation.

• y=a(1-6) (1+4)

• Substitute the "y" value of the vertex for the "y" value in the equation.

• -50=a(1-6) (1+4)

• -50=a(-5) (5)

• -50=a(-25)

• -50/-25=a(-25)/-25

• a=2

 

Therefore, equation is y=2(x-6) (x+4).

 

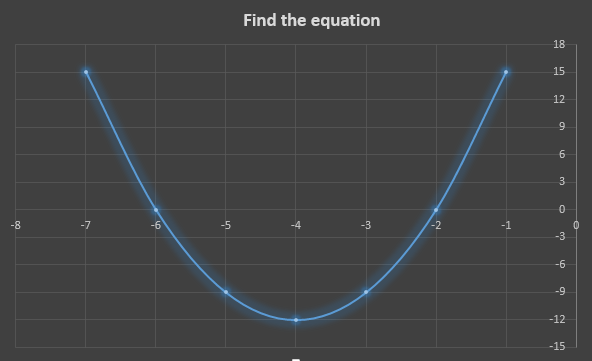
Trial time!

Try this...

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

The answer is...

 

 

 

 

 

y=3(x+6) (x+2)