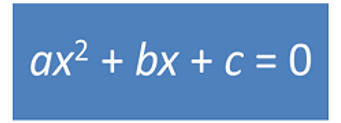Relation between all three forms of quadratics
Vertex form
-
Written as y=a(x-h)^2+k
-
Vertex is the (h,k).
-
Can be changed to standard form by expanding.
-
Can be changed to factored form by finding the x-intercepts and writting it in factored form, or can be changed to standard form and then factored.
-
To find x-intercepts, change y=0, and isolate x.
-
The "h" value is the axis of symmetry.
-
The "k" is the optimal value.
Useful site to test your knowledge-http://www.mathopenref.com/quadvertexexplorer.html
Standard form
-
Written as y=ax^2+bx+c.
-
Use the quadratic formula to find the x-intercepts.
-
Can be changed to factored form by factoring if possible.
-
Can be changed to vertex form by changing it into a perfect square.
-
Axis of symmetry is the average of the x-intercepts.
-
Optimal value can be found by pluging in the axis of symmetry (x) into the original equation.
-
Vertex is the (axis of symmetry, optimal value).
Useful site for extra information-http://www.mathsisfun.com/algebra/standard-form.html
Factored form
-
Written as y=a(x-r) (x-s).
-
The "r" and "s" are the x-intercepts.
-
Axis of symmetry is the average of the two x-intercepts.
-
"x" can be found by setting each bracket equal to 0.
-
Optimal value is found by substituting the axis of symmetry into the original equation.
-
Vertex is (axis of symmetry, optimal value).
-
Can be changed to vertex form by changing it into standard form first, and then changing it into vertex form.
-
Can be changed to standard form by expanding.
Utilize this site to achieve information and examples-http://www.purplemath.com/modules/factquad.htm
“In learning you will teach, and in
teaching you will learn.”